Penrosetriangel
I våre dager er Penrosetriangel et tema som har fått stor aktualitet i dagens samfunn. Folk er stadig mer interessert i å utforske og forstå virkningen Penrosetriangel har på deres daglige liv. Enten fra et personlig, faglig eller sosialt synspunkt, har Penrosetriangel blitt et grunnleggende element som vi ikke kan ignorere. Det er derfor vi i denne artikkelen ønsker å fordype oss i temaet Penrosetriangel, utforske dens forskjellige dimensjoner og prøve å kaste lys over dens betydning i den moderne verden. Vi vil fordype oss i dens opprinnelse, dens utvikling over tid og hvordan den har påvirket måten vi lever og forholder oss til. Uten tvil er Penrosetriangel et fascinerende tema som fortjener å bli analysert i dybden.
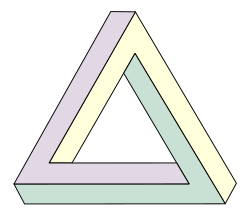

Penrosetriangelet er et umulig objekt. Den svenske kunstneren Oscar Reutersvärd laget bildet av «konstruksjonen» i 1934. Matematikeren Roger Penrose kom til samme idé omkring 1950-årene og beskrev den som «umulighet i sin reneste form». Kunstneren Maurits Cornelis Escher var inne på samme spor og var inspirasjonen til Penroses arbeid[1].
Triangelet gir skinn av å være en solid tredimensjonal figur, laget av tre like lange bjelker som møtes parvis i rette vinkler mot hverandre i hjørnene av en noe skjev sammensetning. Dette lar seg gjøre på papiret, slik illustrasjonen viser, men kan ikke virkeliggjøres i tre dimensjoner.
M.C. Eschers litografi: Vannfall forestiller et vannløp som flyter i sikk-sakk langs langsidene av to forlengede Penrosetriangler, og ender opp to etasjer høyere enn startpunktet. Vannfallene som utgjør kortsidene av trianglene driver vannhjul. Eschers hjelpsomme kommentar var at hvis man ville ha hjulene til å fortsette å snurre, trengtes påfyll av og til for å kompensere for fordampningen.
Hvis man trekker en midtlinje langs sidene i dette triangelet, vil man til slutt komme tilbake til utgangspunktet. Figuren er en tre-vridd möbiusstripe.
En tilsvarende umulig figur er Penrosetrappa.
Andre Penrosepolygoner
Den visuelle virkningen avtar med å innføre flere hjørner.
Referanser
Eksterne lenker
- (en) Penrose triangles – kategori av bilder, video eller lyd på Commons
- Escher for Real constructions
- Three-dimensional model of a Penrose triangle for SketchUp Arkivert 18. oktober 2012 hos Wayback Machine.



